SVM

支持向量机

有监督学习
分类
回归
判别式模型
训练完成后，大部分训练样本都不需要保留，最终模型仅与支持向量有关

支持向量机是一种有监督学习算法，既可以用于分类，也可以用于回归。

最初SVM被提出用于二类分类问题。

支持向量机是判别分类方法，用一条分割线（二维空间中的直线或曲线）或流形体（多维空间中的曲线、曲面等概念的推广）将各种类型分割开。

基本思想

在特征空间中寻找间隔最大的分离超平面将数据高效地分为两类。

正确划分数据集
分离超平面几何间隔最大

类别

线性可分支持向量机

训练样本线性可分
通过硬间隔最大化，学习一个线性分类器

线性支持向量机

训练样本近似线性可分
引入松弛变量，通过软间隔最大化，学习一个线性分类器

非线性支持向量机

训练样本线性不可分
通过使用核函数及软间隔最大化，学习一个分类器

原理

考虑样本容量为$n$的训练数据集
$$S=\lbrace(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\cdots,(\mathbf{x}_n,y_n)\rbrace$$

$\mathbf{x}_i\in \mathbb{R}^p$为第$i$个样本（$i=1,\cdots,n$）
$x_j$为第$j$个特征（$j=1,\cdots,p$）
$y_i\in\lbrace+1,-1\rbrace$为第$i$个样本的标签（$i=1,\cdots,n$）

线性可分

假设训练数据集线性可分的。

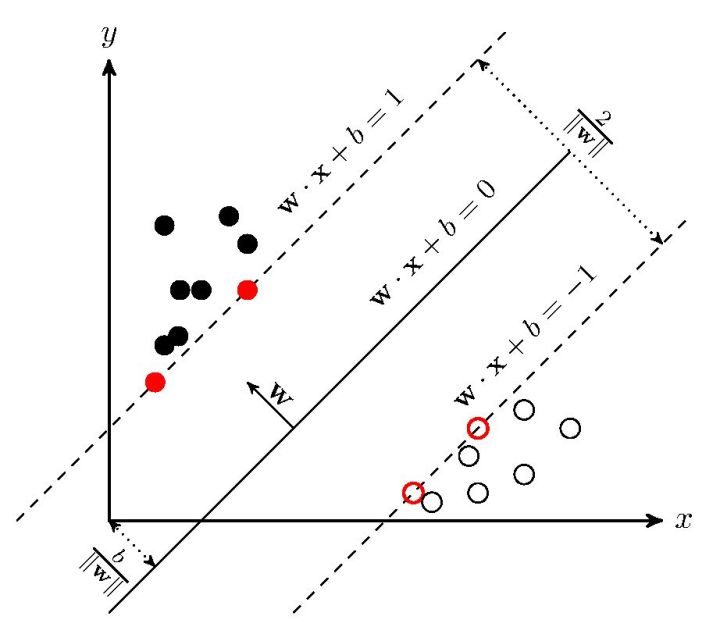
几何间隔：对于给定的数据集$S$和超平面 $\mathbf{w}\cdot \mathbf{x}+b=0$，超平面关于样本点$(\mathbf{x}_i,y_i)$的几何间隔为
$$\gamma_i=y_i\left(\frac{\mathbf{w} }{||\mathbf{w}||}\cdot\mathbf{x}_i+\frac{b}{||\mathbf{w}||} \right)$$
支持向量（Support Vector）：在线性可分情况下，训练数据集中与分离超平面距离最近的样本点的实例称为支持向量
- 即：满足约束条件$y_i(\mathbf{w}\cdot\mathbf{x}_i+b)=1$的样本点实例
- $y_i=+1$的正例点，支持向量在超平面$H_1:\mathbf{w}\cdot\mathbf{x}+b=1$上
- $y_i=-1$的负例点，支持向量在超平面$H_2:\mathbf{w}\cdot\mathbf{x}+b=-1$上
间隔（margin）：超平面$H_1$和$H_2$之间的距离，等于
$$\frac{2}{||\mathbf{w}||}$$

超平面$\mathbf{w}\cdot \mathbf{x}+b=0$关于所有样本点的几何间隔最小值为
$$\gamma=\min_{i=1,\cdots,n}\gamma_i$$
即支持向量到超平面的距离。

因此，求解“最大分割超平面问题”即求解下列带约束的最优化问题
$$\max_{\mathbf{w},b}\gamma\quad \mathrm{s.t.}\quad y_i\left(\frac{\mathbf{w} }{||\mathbf{w}||}\cdot\mathbf{x}_i+\frac{b}{||\mathbf{w}||} \right)\geq \gamma,\quad i=1,\cdots,n$$

等价于
$$y_i\left(\frac{\mathbf{w} }{||\mathbf{w}||\gamma}\cdot\mathbf{x}_i+\frac{b}{||\mathbf{w}||\gamma} \right)\geq1,\quad i=1,\cdots,n$$
令

$$\mathbf{w}\triangleq\frac{\mathbf{w} }{||\mathbf{w}||\gamma}$$
$$b\triangleq\frac{b}{||\mathbf{w}||\gamma}$$
则约束问题为

$$y_i(\mathbf{w}\cdot \mathbf{x}_i+b)\geq1,\quad i=1,\cdots,n.$$

$$\max{\gamma}\Longleftrightarrow\max{\frac{1}{||\mathbf{w}||} }\Longleftrightarrow\min\frac{1}{2}||\mathbf{w}||^2$$

因此，SVM模型“求解最大分割超平面问题”即求解以下带约束条件的最优化问题

$$\min_{\mathbf{w},b} \frac{1}{2}||\mathbf{w}||^2$$
$$\mathrm{s.t.}\quad y_i( \mathbf{w}^T \mathbf{x}_i+b)\geq 1, \forall i$$

$\mathbf{w}$是超平面参数。

使用拉格朗日乘子法求解上述有约束条件的最优化问题

$$L( \mathbf{ w } ,b, \mathbf{ \lambda } )=\frac{ 1 }{ 2 } || \mathbf{ w } ||^2 - \sum_{ i=1 }^n \lambda_i \left[ y_i ( \mathbf{ w }^T \mathbf{ x }_i + b ) - 1 \right] $$

其中，$\lambda_i$为拉格朗日乘子，且$\lambda_i \geq 0$。

令
$$\theta( \mathbf{w} )=\max_{ \lambda_i \geq 0 } L ( \mathbf{w} , b, \mathbf{ \lambda } )$$

当样本点不满足约束条件时，即$y_i( \mathbf{w}^T \mathbf{x}_i + b)<1$，将$\lambda_i$设置为无穷大，则$\theta( \mathbf{w} )$也为无穷大
当样本点满足约束条件时，即$y_i (\mathbf{w}^T \mathbf{x}_i + b) \geq 1$，将$\theta( \mathbf{w} )$设置为原函数本身

即
$$
\theta(\mathbf{w})=
\left\lbrace
\begin{array}{ll}
\frac{1}{2} || \mathbf{ w } || ^2, & \mathbf{x} \in 可行区域 \\
+ \infty, & \mathbf{ x } \in 不可行区域
\end{array}
\right.
$$

因此，约束问题等价于

$$\min_{ \mathbf{w} ,b} \theta( \mathbf{w} ) = \min_{ \mathbf{w}, b} \max_{ \lambda_1 \geq 0} L( \mathbf{w} , b, \mathbf{ \lambda} )=p^*$$

由拉格朗日函数的对偶性可得
$$\max_{ \lambda_1 \geq 0}\min_{ \mathbf{w} , b } L ( \mathbf{w} , b , \mathbf{\lambda})=d^*$$

要使得$ p^* = d^* $，需满足：

优化问题是凸优化问题
本优化问题是一个凸优化问题
满足KKT条件
即要求
$$\left\lbrace
\begin{array}{l}
\lambda_i \geq 0 \\
y_i( \mathbf{ w }_i \cdot \mathbf{x}_i + b )-1 \geq 0 \\
\lambda_i \left[ y_i ( \mathbf{ w }_i \cdot \mathbf{ x }_i + b ) - 1 \right] = 0 \\
\end{array}
\right.$$

令

$$\frac{\partial L(\mathbf{ w },b, \lambda )}{ \partial \mathbf{w} }=0,\quad \frac{\partial L(\mathbf{w},b,\lambda)}{\partial b} = 0 $$

可得

$$
\left\lbrace
\begin{array}{l}
\mathbf{ w } = \sum_{ i=1 }^n \lambda_i y_i \mathbf{ x }i \\
\sum{ i = 1 }^n \lambda_i y_i = 0 \\
\end{array}
\right.
$$

代入 $L ( \mathbf{ w } , b, \lambda )$ 消去 $ \mathbf{ w }$ 和 $b$ 得

$$
\begin{aligned}
L( \mathbf{ w },b,\lambda) &= \frac{1}{2} \sum_{ i=1 }^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j ( \mathbf{ x }i \cdot \mathbf{ x }j ) - \sum{i=1}^n \lambda_i y_i \left[ \left( \sum{ j=1 }^n \lambda_j y_j \mathbf{ x }j \right) \cdot \mathbf{x}i + b \right] + \sum{i=1}^n \lambda_i \\
&= -\frac{1}{2} \sum_{i=1}^n \sum{j=1}^n \lambda_i \lambda_j y_i y_j ( \mathbf{ x }_i \cdot \mathbf{ x }j ) + \sum{i=1}^n \lambda_i \\
\end{aligned}
$$

则

$$\min_{\mathbf{ w } , b} L ( \mathbf{w} , b, \mathbf{ \lambda } ) = - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j ( \mathbf{x}_i \cdot \mathbf{x}j )+ \sum{i=1}^n \lambda_i $$

那么

$$\max_{ \lambda } \min_{ \mathbf{ w } , b } L ( \mathbf{ w },b, \mathbf{ \lambda })$$

等价于

$$
\begin{aligned}
\max_{ \lambda } & - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j ( \mathbf{ x }_i \cdot \mathbf{ x }j ) + \sum{i=1}^n \lambda_i \\
\mathrm{ s.t. } & \sum_{ i = 1 }^n \lambda_i y_i = 0 \\
& \lambda_i \geq 0 , \quad i = 1 , \cdots , n. \\
\end{aligned}
$$

使用序列最小化算法（SMO）（待补充）求解上述优化问题。

通过SMO算法求解得到最优$\pmb{ \lambda }^*$，从而求解出$\mathbf{w}$和$b$，进而求得最优超平面——决策平面。

在$\pmb{ \lambda }^* $中，至少存在一个$ \lambda_j^* > 0$

证明（反证法）：若不存在$ \lambda_j^* > 0$，则$ \mathbf{ w } = 0 $，矛盾

对$\lambda_j^* > 0$有

$$y_j \left( \mathbf{ w }^* \cdot \mathbf{ x }_j+b^* \right)-1=0$$

因此

$$
\begin{aligned}
\mathbf{ w }^{ * } &= \sum_{i=1}^n \lambda_i^{ * } y_i \mathbf{ x }_i \\
b^{ * } &= y_j-\sum_{ i=1 }^n \lambda_i^{ * } y_i ( \mathbf{ x }_i \cdot \mathbf{ x }_j ) \\
\end{aligned}
$$

对于任意训练样本$(\mathbf{x}_i,y_i)$，总有$\lambda_i=0$或$y_i \left( \mathbf{ w }^* \cdot \mathbf{x}_i + b^* \right) = 1$。

若$\lambda_i=0$，则该样本不会出现在求解“决策平面”参数得式子中
若$\lambda_i>0$，则必有$ y_i \left( \mathbf{ w }^* \cdot \mathbf{ x }_i + b^* \right) = 1$，即样本点位于最大间隔边界上—— $(\mathbf{ x }_i,y_i ) $是一个支持向量

近似线性可分

实际情况下，几乎不存在完全线性可分的数据，对于近似线性可分的训练数据集，引入软间隔——允许某些点不满足约束$y_i(\mathbf{w}\cdot\mathbf{x}_i+b)\geq 1$

引入松弛变量(Hinge损失函数)$ \xi_i = \max \lbrace 0 , 1 - y_i( \mathbf{ w } \cdot \mathbf{x}_i + b) \rbrace$，将原优化问题改写为

$$
\begin{aligned}
\min_{ \mathbf{w} , b , \xi } & \quad \frac{1}{2} || \mathbf{ w } ||^2+ \phi \sum_{i=1}^n \xi_i \\
\mathrm{s.t.} & \quad y_i ( \mathbf{ w } \cdot \mathbf{ x }_i + b ) \geq 1- \xi_i \\
& \quad \xi_i \geq 0,\quad i=1,\cdots,n. \\
\end{aligned}
$$

其中$\phi$为惩罚参数，$\phi$越大，对分类的惩罚越大。

非线性SVM

通过非线性变换将非线性分类问题转化为线性分类问题。

用核函数替换线性SVM中的内积

核函数（Kernel function）：存在一个从输入空间到特征空间的映射$\varphi(\cdot)$，对输入空间中的任意两点$x,z$有
$$K(x,z)=\varphi(x) \cdot \varphi(z)$$

则分类决策函数变为
$$f(\mathbf{x})=\mathrm{sign} \left( \sum_{i=1}^n \lambda_i^* y_i K ( \mathbf{ x }, \mathbf{ x }_i ) + b^* \right)$$

算法

线性支持向量机

综合原理章节的讨论，总结线性支持向量机学习算法如下：

输入：训练数据集
$$S=\lbrace ( \mathbf{x}_1 , y_1 ), ( \mathbf{ x }_2 , y_2 ), \cdots , ( \mathbf{ x }_n,y_n ) \rbrace$$
$\mathbf{x}_i\in \mathbb{R}^p$为第$i$个样本（$i=1,\cdots,n$）
$x_j$为第$j$个特征（$j=1,\cdots,p$）
$y_i\in \lbrace +1, -1 \rbrace$为第$i$个样本的标签（$i=1,\cdots,n$）
输出：分离超平面、分类决策函数

选择惩罚参数 $\phi > 0 $，构造并求解凸二次规划问题

$$
\begin{aligned}
\min_{ \pmb{ \lambda } } & \quad \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j ( \mathbf{x}_i \cdot \mathbf{ x }j ) -
\sum{i=1}^n \lambda_i \\
\mathrm{s.t.} & \quad \sum_{i=1}^n \lambda_i y_i=0 \\
& \quad 0 \leq \lambda_i \leq \phi,\quad i=1,\cdots,n. \\
\end{aligned}
$$

得到最优解

$$\pmb{ \lambda }^* = ( \lambda_1^* ,\cdots ,\lambda_n^* )^T $$
计算
$$\mathbf{w}^* = \sum_{i=1}^n \lambda^*_i y_i \mathbf{ x }_i $$

选择 $\pmb{ \lambda }^* $ 的一个满足条件 $ 0 < \lambda_j^* < \phi $ 的分量 $ \lambda_j^* $，计算

$$ b^* = y_j - \sum_{i=1}^n \lambda_j^* y_j ( \mathbf{x}_i \cdot \mathbf{x}_j ) $$
求分离超平面
$$ \mathbf{w}^* \cdot \mathbf{ x } + b^* = 0 $$
分类决策函数为
$$f( \mathbf{x} ) = \mathrm{ sign }{ ( \mathbf{ w }^* \cdot \mathbf{ x } + b^* ) }$$

非线性支持向量机

输入：训练数据集
$$S = \lbrace ( \mathbf{x}_1 , y_1),( \mathbf{x}_2,y_2),\cdots,( \mathbf{x}_n , y_n ) \rbrace$$
$\mathbf{x}_i \in \mathbb{R}^p $为第$i$个样本（$i=1,\cdots,n$）
$x_j$为第$j$个特征（$j=1,\cdots,p$）
$y_i \in \lbrace +1,-1 \rbrace $为第$i$个样本的标签（$i=1,\cdots,n$）
输出：分离超平面、分类决策函数

选择适当的核函数$K(x,z)$和惩罚参数$\phi>0$，构造并求解凸二次规划问题

\begin{aligned}
\min_{ \pmb{\lambda} } & \quad \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j K( \mathbf{x_i},
\mathbf{x}j ) -
\sum{i=1}^n \lambda_i \\
\mathrm{s.t.} & \quad \sum_{i=1}^n \lambda_i y_i = 0 \\
& \quad 0 \leq \lambda_i \leq \phi ,\quad i=1 ,\cdots , n.
\end{aligned}

得到最优解

$$\pmb{ \lambda }^* = ( \lambda_1^* , \cdots ,\lambda_n^* )^T $$
选择$\pmb{ \lambda }^*$的一个满足条件$ 0 < \lambda_j^* < \phi $的分量$\lambda_j^*$，计算
$$ b^* = y_j - \sum_{i=1}^n \lambda_j^* y_j K( \mathbf{x}_i, \mathbf{x}_j )$$
分类决策函数为
$$f( \mathbf{ x } )=\mathrm{ sign }{ \left( \sum_{i=1}^n \lambda_i^* y_i K( \mathbf{ x }, \mathbf{ x }_i)+b^* \right) }$$

核函数

SVM使用核函数的过程实质是进行特征转换的过程

线性核

多项式核

RBF核

高斯核函数/高斯径向基函数（Radial Basis Function）
$$ K(x,z)=\exp \left( - \frac{ ||x-z||^2 }{ 2 \sigma^2 } \right) $$

对应的SVM是高斯径向基函数分类器
对应的分类决策函数为
$$f(\mathbf{ x }) = \mathrm{ sign }{ \left( \sum_{i=1}^n \lambda_i^* y_i \exp{ \left( - \frac{ || \mathbf{x} - \mathrm{x}_i ||^2 }{ 2\sigma^2 } \right) } + b^* \right) }$$

核函数	形式	优点	缺点	适用情形
线性核	$\mathbf{x}_i^T\mathbf{x}_j$	高效实现，不易过拟合	无法解决非线性可分问题	$p\gg n$（如：文本分类问题）
多项式核	$(\beta\mathbf{x}_i^T\mathbf{x}_j+\theta)^n$	比线性核更一般，$n$直接描述了被映射空间的复杂度	参数多，当$n$很大时会导致计算不稳定
RBF核	$\exp{\left(-\frac{\|\|\mathbf{x}_i-\mathbf{x}_j\|\|^2}{2\sigma^2} \right)}$	只有一个参数，没有计算不稳定问题	计算慢，过拟合风险大	$p$较小、$n$中等

其中

$n$：样本数
$p$：特征维度

当 $p$ 较小、$n$ 较大时，支持向量机性能通常不如深度神经网络

总结

若样本的某些特征数据缺失，可能会影响SVM模型训练结果的好坏。

SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM的性能很重要

优点

SVM的优点：

模型以来的支持向量比较少，消耗内存少
预测阶段的速度快
模型只受边界线附近的点的影响，因此对于高维数据的学习效果非常好
与核函数方法的配合极具通用性，能够适用于不同类型的数据（不仅适用于线性问题，还适用于非线性问题）
SVM是一个凸优化问题，所以求得的解是全局最优而不是局部最优
理论基础比较完善
通过调参往往可以得到很好的分类效果
泛化能力好
SVM对线性不可分的数据有较好的分类性能

缺点

SVM的缺点：

随着样本量 $N$ 的增加，模型的训练复杂度可能会高达 $\mathcal{ O }( N^3 )$，即使经过高效处理后，复杂度也有 $\mathcal{ O }( N^2 )$。即，大样本下模型学习的计算成本会很高。
训练效果非常依赖于边界软化参数$C$的选择是否合理；需要通过交叉检验进行检索；当数据集较大时，计算量也很大
SVM对缺失数据敏感
非线性问题的核函数的选择没有通用标准，难以选择一个合适的核函数

支持向量回归机

SVR
Support Vector Regression

SVM本身是针对二分类问题提出的
SVR是SVM的一个重要的应用分支

SVR与SVM的区别在于：

SVR的样本点只有一类，所寻求的最优超平面是使所有的样本点离该超平面的总偏差最小

SVM vs LR

SVM：支持向量机
LR：逻辑回归

最本质的区别：损失函数不同

	支持向量机	逻辑回归
相同点	都是分类算法(也都可以用于回归)
	（如果不考虑核函数）分类决策面都是线性的原始的LR和SVM都是线性分类器
	都是监督学习算法
	都是Post not found: 生成式模型-判别式模型判别式模型
损失函数	Hinge Loss	Log-Loss
目标	最大化分割超平面距离	最大化数据分到正确的类的概率
样本点	只考虑局部的边界线附近的点	考虑所有点（全局）
数据分布	不直接依赖于数据分布	受所有数据点的影响
非线性问题	使用核函数	不适用核函数
正则化	线性SVM依赖数据的距离测度，需要先对数据进行归一化（Normalization）	不需要事先Normalization
正则项	损失函数自带正则项$\frac{1}{2}\|\|\mathbf{w}\|\|^2$	需要另外添加正则项

考虑标签为$y\in\lbrace 0,1\rbrace$的LR和SVM。
LR的决策函数可以为

$$
\hat{y}=\left\lbrace
\begin{array}{ll}
1 & \mathrm{if} P(y=1|x) \geq P(y=0|x) \\
0 & \mathrm{otherwise} \\
\end{array}
\right.
$$

其中
$$
\begin{aligned}
P(y=1|x) & \propto \exp{ ( \mathbf{w}^T \cdot \mathbf{x} + b ) } \\
P(y=0|x) & \propto 1 \\
\end{aligned}
$$

如果我们只是想做出正确决策，而不是获得每个类别的概率，可以用似然比来进行决策
$$ \frac{ P( y=1|x ) }{ P( y=0|x ) } \geq c,\quad c > 1 $$
上述不等式两边同取对数，得
$$\log{ ( P(y=1|x))}- \log{(P(y=0|x))} \geq \log{c}$$
则有
$$\exp{ ( \mathbf{w}^T \cdot \mathbf{x} + b ) } \geq \log{c}$$
因为$c$是任意常数，所以我们可取 $c$ 满足 $\log{c}=1$，使得
$$\exp{ ( \mathbf{w}^T \cdot \mathbf{ x } + b ) } \geq 1$$

上式可能存在多个解，如果添加一个二次惩罚项进行约束，则能使解唯一：
$$
\begin{aligned}
\min & \quad \frac{1}{2} || \mathbf{w}||^2 \\
\mathrm{s.t.} & \quad (2 y_i - 1 )( \mathbf{w}^T \mathbf{x}_i + b ) \geq 1,\quad \forall i=1,\cdots,n. \\
\end{aligned}
$$

注意这里考虑的 $ y_i \in \lbrace 0,1 \rbrace $ ，而不是前面的 $y_i \in \lbrace -1, +1 \rbrace$ ，因此约束条件中是 $(2 y_i-1)$ 而不是 $y_i$。

添加了约束条件后，得到的是SVM！

We derived an SVM by asking LR to make the right decisions. ——from Support Vector Machines vs Logistic Regression

多分类

多分类逻辑回归（Multi-class LR）
$$ P(y=i|x)=\frac{ \exp{ ( w_i^T x + b_i ) } }{ \sum_{j} \exp{ ( w_j^T x + b_j ) } } $$
多分类支持向量机（Multi-class SVM）
$$ \frac{ P(y=i|x) }{ P( y = k| x ) } \geq c \quad \forall \quad k \neq i$$
即
$$ w_i^T x - w_k^T x \geq 1 \quad \forall \quad k\neq i $$

选择SVM还是LR？

参考Support Vector Machines vs Logistic Regression

As always, depends on your problem.
LR gives calibrated probabilities that can be interpreted as confidence in a decision.
LR gives us an unconstrained, smooth objective.
SVMs don’t penalize examples for which the correct decision is made with sufficient confidence. 有利于泛化
SVMs have a nice dual form（对偶形式）, giving sparse solutions when using the kernel trick (better scalability 良好的伸缩性)

Python实现

简单分类数据：

import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

## 创建类别数为2的分类数据
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

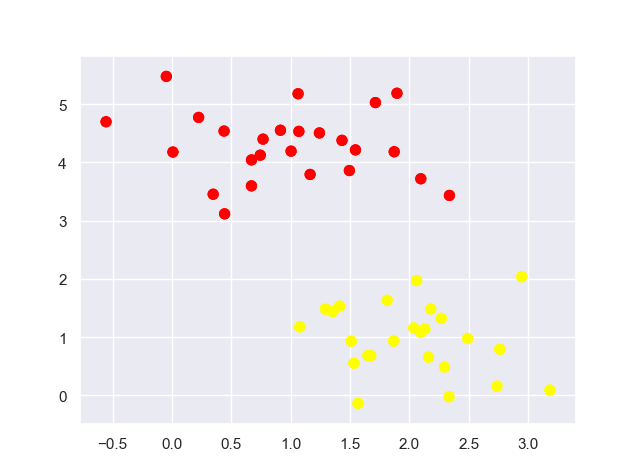
简单分割线：

import numpy as np
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)  ##特殊点

for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
    plt.plot(xfit, m * xfit + b, '-k')  ##画三条分割直线

plt.xlim(-1, 3.5)

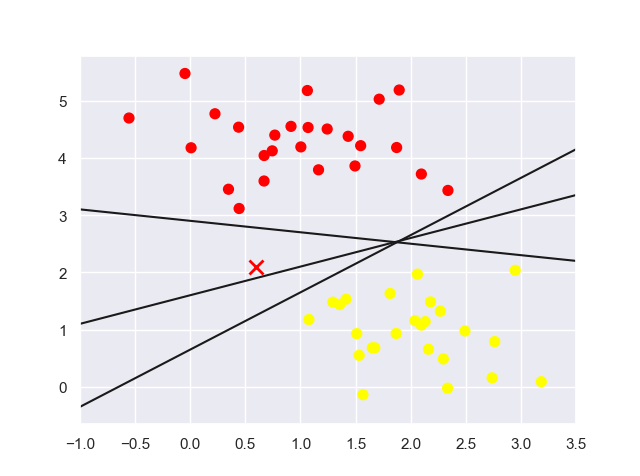
上图中的三条简单分割直线（分割器）都能很好地判别这些样本（每条直线都能将圆点数据点正确地分为两类）。但是对于点“X”，不同的分割器将其分配到不同的标签。

若将分割直线变成具有宽度的、到最近点边界的线条，如下图：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
    yfit = m * xfit + b
    plt.plot(xfit, yfit, '-k')
    plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none', color='#AAAAAA', alpha=0.4)

plt.xlim(-1, 3.5)

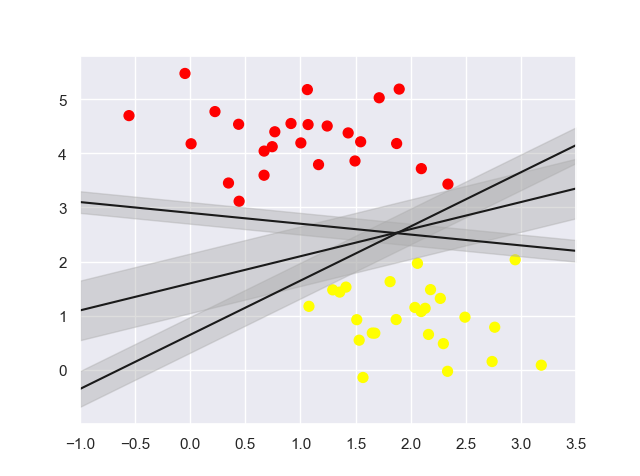
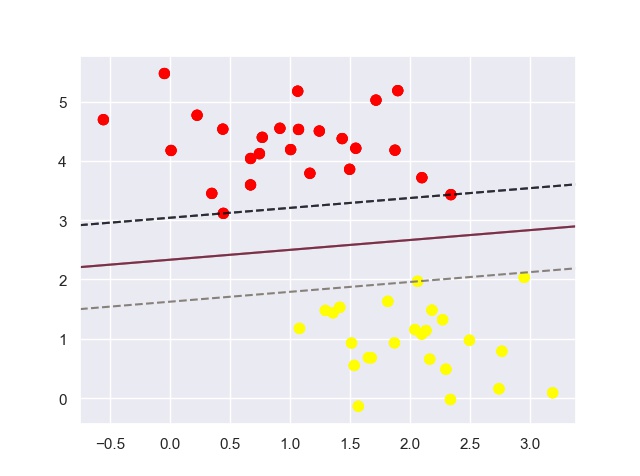
正好在边界线上的点，被称为支持向量。

在scikit-learn中，支持向量的坐标存放在分类器的support_vectors_属性中。

SVM对远离边界的数据点不敏感。

Skye

Machine Learning | 支持向量机 // Support Vector Machine