Skye
0%

Kaggle | House Prices:Advanced Regression Techniques

发表于 更新于 Valine：

汇总请见：数据清洗合集

House Prices: Advanced Regression Techniques

数据来源：Kaggle

代码参考：COMPREHENSIVE DATA EXPLORATION WITH PYTHON

进行数据分析前的主要工作：

  1. 理解问题 Understanding the problem
    • 看每个变量的含义和重要性
  2. 进行单变量探究 Univariate study
    • 关注因变量
  3. 进行多变量探究 Multivariate study
    • 因变量与自变量间的关系
  4. 简单数据清洗 Basic cleaning
    • 数据缺失
    • 异常点
    • 分类变量的处理
  5. 检验假设 Test assumptions

载入数据

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings

warnings.filterwarnings("ignore")
%matplotlib inline
1
2
df_train = pd.read_csv("train.csv")
df_train.columns
Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
       'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
       'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
       'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
       'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
       'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
       'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
       'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
       'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
       'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
       'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
       'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
       'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
       'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
       'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
       'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
       'SaleCondition', 'SalePrice'],
      dtype='object')

'SalePrice’是因变量

描述性统计

1
df_train['SalePrice'].describe()
count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64
  • 'SalePrice’最小值应该为正（$\surd$）
  • 最小值和最大值相差较大
1
2
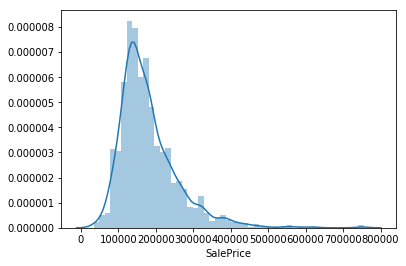
## 直方图
sns.distplot(df_train['SalePrice'])
<matplotlib.axes._subplots.AxesSubplot at 0x16f6ce68828>
  • 'SalePrice’集中分布在300000以下
  • 右偏
1
2
3
## 计算‘SalePrice’的偏度和峰度
print('Skewness: %f' % df_train['SalePrice'].skew())  ## 偏度
print('Kurtosis: %f' % df_train['SalePrice'].kurt())  ## 峰度
Skewness: 1.882876
Kurtosis: 6.536282
  • 偏度大于0——右偏
  • 峰度大于3——厚尾

探究变量之间的关系

1
2
3
4
5
6
## GrLivArea: Above grade (ground) living area square feet
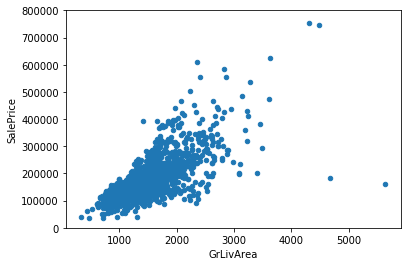
## ‘GrLivArea’与‘SalePrice’的散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]],
                axis=1)  ## 按列合并
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))
<matplotlib.axes._subplots.AxesSubplot at 0x16f6d629978>

'GriLivArea’与’SalePrice’之间具有明显的线性关系

1
2
3
4
5
6
##  TotalBsmtSF：Total square feet of basement area
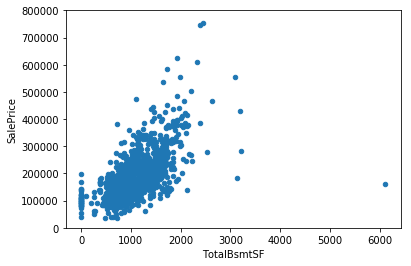
## ‘TotalBsmtSF’与‘SalePrice’的散点图
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]],
                axis=1)  ## 按列合并
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))
<matplotlib.axes._subplots.AxesSubplot at 0x16f6d6eacc0>
  • ‘TotalBsmtSF’与‘SalePrice’之间也具有明显的线性关系
  • 一些样本中，‘TotalBsmtSF’为零
1
2
3
4
5
6
7
8
9
10
## OverallQual: Rates the overall material and finish of the house
## 'OverallQual'与‘SalePrice’的箱线图
## 'OverallQual'是分类变量，有1~10共10个取值
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], 
                axis=1)

f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000)
(-0.5, 9.5, 0, 800000)
  • "OverallQual"越高，"SalePrice"的值相对越大
  • "OverallQual"较高的"SalePrice"的分布较为分散
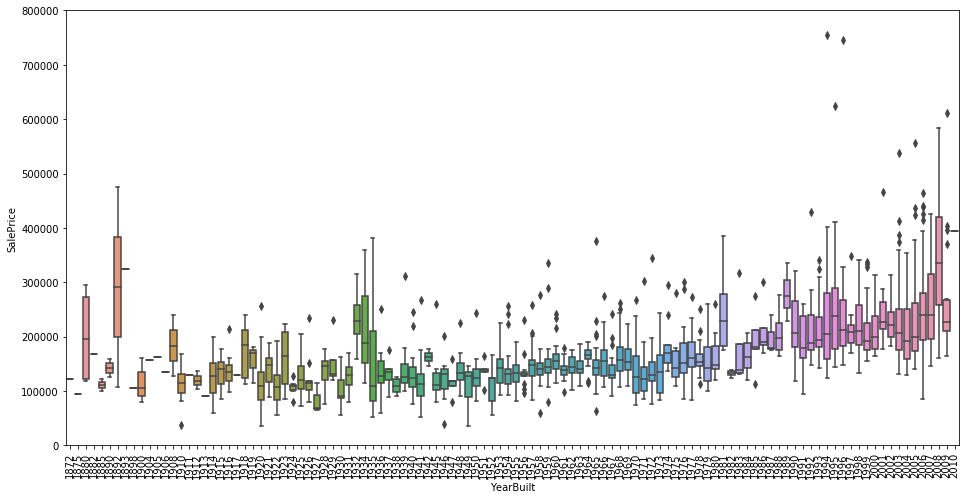
1
2
3
4
5
6
7
8
9
## YearBuilt: Original construction date
var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], 
                axis=1)

f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000)
plt.xticks(rotation=90)  ## x轴的刻度旋转90度（即垂直于x轴）
(array([  0,   1,   2,   3,   4,   5,   6,   7,   8,   9,  10,  11,  12,
         13,  14,  15,  16,  17,  18,  19,  20,  21,  22,  23,  24,  25,
         26,  27,  28,  29,  30,  31,  32,  33,  34,  35,  36,  37,  38,
         39,  40,  41,  42,  43,  44,  45,  46,  47,  48,  49,  50,  51,
         52,  53,  54,  55,  56,  57,  58,  59,  60,  61,  62,  63,  64,
         65,  66,  67,  68,  69,  70,  71,  72,  73,  74,  75,  76,  77,
         78,  79,  80,  81,  82,  83,  84,  85,  86,  87,  88,  89,  90,
         91,  92,  93,  94,  95,  96,  97,  98,  99, 100, 101, 102, 103,
        104, 105, 106, 107, 108, 109, 110, 111]),
 <a list of 112 Text xticklabel objects>)

不知“SalePrice”是否已剔除通胀影响的价格，无法对不同建造年份的房屋价格进行比较。

1
2
3
4
5
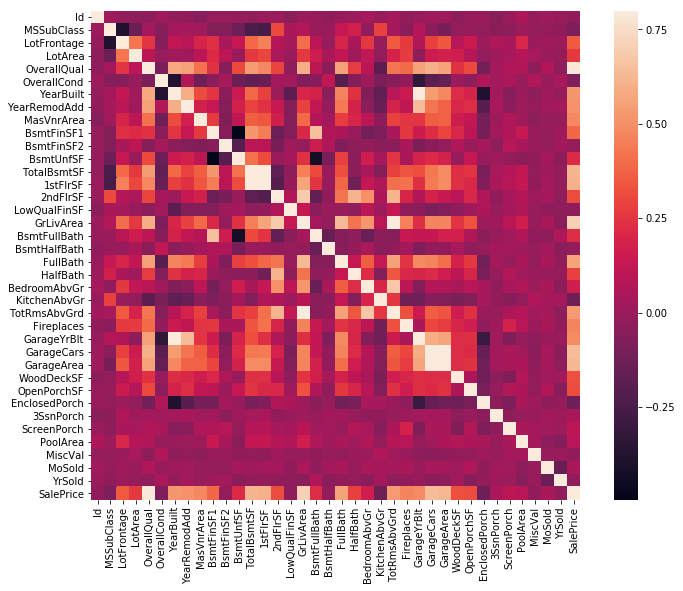
## 相关系数阵
cor_m = df_train.corr()

f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(cor_m, vmax=.8, square=True)
<matplotlib.axes._subplots.AxesSubplot at 0x16f6f3a2da0>
  • 颜色越浅，表明正相关性越强
    • 'TotalBsmtSF’和’1stFlrSF’的正相关性很强（很显然）
    • 'GarageCars’和’GarageArea’的正相关性很强（也很显然）
  • 上述两组正相关性很强的变量，导致数据存在多重共线性
    • 考虑剔除其中一个变量，因为正相关性强的两个变量包含的信息是相似的
  • 看‘SalePrice’那一列，也可以通过热力图的颜色深浅，直观地发现与‘SalePrice’正相关性较强的变量，如‘OverallQual’、‘GriLivArea’

其中：

  • 1stFlrSF: First Floor square feet
  • TotalBsmtSF: Total square feet of basement area
  • GarageCars: Size of garage in car capacity
  • GarageArea: Size of garage in square feet
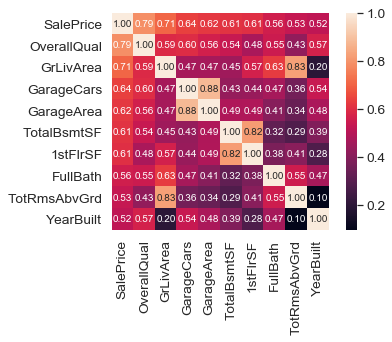
1
2
3
4
5
6
7
8
9
10
11
## 放大相关系数矩阵热力图的部分
## 相关系数最大的10个变量
k = 10
cols = cor_m.nlargest(k, 'SalePrice')['SalePrice'].index
cm = np.corrcoef(df_train[cols].values.T)

sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True,
                fmt='.2f', annot_kws={'size': 10},
                yticklabels=cols.values, xticklabels=cols.values)
plt.show()

相关性较强的几对变量：

  • ‘GarageCars’、‘GarageArea’
  • ‘GriLivArea’、‘TotRmsAbvGrd’
  • ‘TotalBsmtSF’、‘1stFlrSF’

考虑剔除每对中的一个

1
2
3
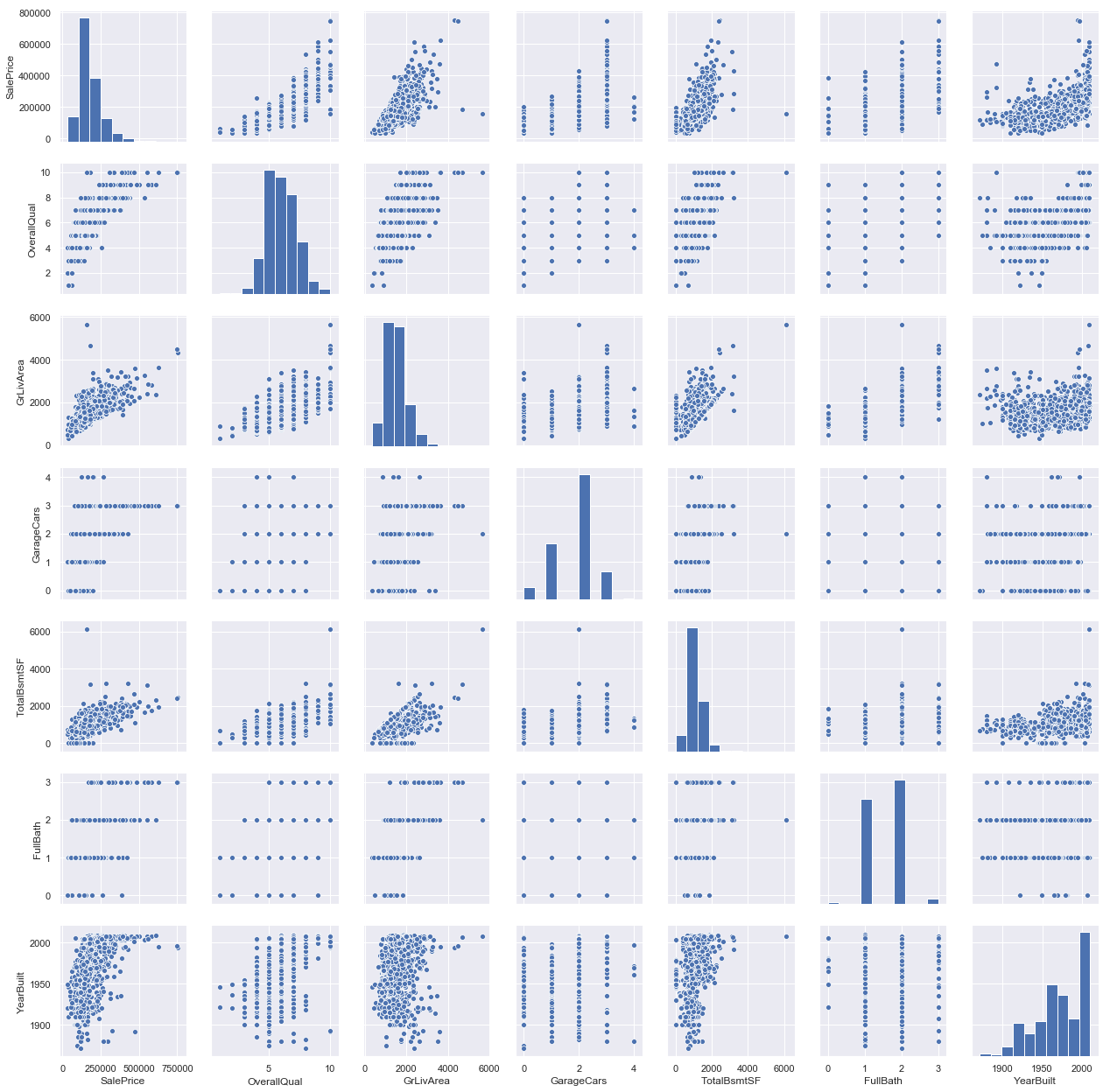
4
5
6
## 散点图
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 
        'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size=2.5)
plt.show()

数据清洗

缺失

1
2
3
4
5
6
## 统计每列的缺失数据个数，并按降序排列
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1,
                        keys=['Total', 'Percent'])
missing_data.head(20)  ## 缺失数据最多的20个列
Total Percent
PoolQC 1453 0.995205
MiscFeature 1406 0.963014
Alley 1369 0.937671
Fence 1179 0.807534
FireplaceQu 690 0.472603
LotFrontage 259 0.177397
GarageCond 81 0.055479
GarageType 81 0.055479
GarageYrBlt 81 0.055479
GarageFinish 81 0.055479
GarageQual 81 0.055479
BsmtExposure 38 0.026027
BsmtFinType2 38 0.026027
BsmtFinType1 37 0.025342
BsmtCond 37 0.025342
BsmtQual 37 0.025342
MasVnrArea 8 0.005479
MasVnrType 8 0.005479
Electrical 1 0.000685
Utilities 0 0.000000
  • 当一个列的数据超过15%都是缺失，则应考虑删除该列
  • 列’PoolQC’, ‘MiscFeature’, 'Alley’等的缺失比例较大，考虑删除
  • ‘GarageX’几个列的缺失个数一样，但是缺失比例都较小
  • ‘BsmtX’几个列的缺失个数也一样
1
2
3
4
5
## 考虑删除上述存在缺失值的列（除了‘Electrical’）
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index, 1)
## 删除‘Electrical’缺失的样本
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max()  ## 检查是否还存在缺失
0

异常点

1
2
3
4
5
6
7
8
## 标准化
SalePrice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:, np.newaxis])
low_range = SalePrice_scaled[SalePrice_scaled[:, 0].argsort()][:10]
high_range = SalePrice_scaled[SalePrice_scaled[:, 0].argsort()][-10:]
print('Outer range (low) of the distribution:')
print(low_range)
print('\nOuter range (high) of the distribution:')
print(high_range)
Outer range (low) of the distribution:
[[-1.83820775]
 [-1.83303414]
 [-1.80044422]
 [-1.78282123]
 [-1.77400974]
 [-1.62295562]
 [-1.6166617 ]
 [-1.58519209]
 [-1.58519209]
 [-1.57269236]]

Outer range (high) of the distribution:
[[3.82758058]
 [4.0395221 ]
 [4.49473628]
 [4.70872962]
 [4.728631  ]
 [5.06034585]
 [5.42191907]
 [5.58987866]
 [7.10041987]
 [7.22629831]]
  • 较低的10个值仅在-1.5到-1.9之间
  • 而较高的10个值的跨度从3到7.5
  • 要小心SalePrice标准化后值为7以上的样本点
1
2
3
4
5
6
## 再来看看该图
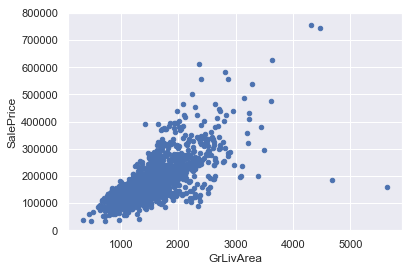
## ‘GrLivArea’与‘SalePrice’的散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]],
                axis=1)  ## 按列合并
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000))
'c' argument looks like a single numeric RGB or RGBA sequence, which should be avoided as value-mapping will have precedence in case its length matches with 'x' & 'y'.  Please use a 2-D array with a single row if you really want to specify the same RGB or RGBA value for all points.





<matplotlib.axes._subplots.AxesSubplot at 0x16f736e0ac8>

观察上图，可以发现右上方和右下方各有2个点较为异常。

  • 右上方的两个点比较顺应整体趋势
  • 而右下方的两个点并没有顺应整体趋势，考虑将其删去
1
2
## 删除异常点
df_train.sort_values(by='GrLivArea', ascending=False)[:2]
Id MSSubClass MSZoning LotArea Street LotShape LandContour Utilities LotConfig LandSlope ... EnclosedPorch 3SsnPorch ScreenPorch PoolArea MiscVal MoSold YrSold SaleType SaleCondition SalePrice
1298 1299 60 RL 63887 Pave IR3 Bnk AllPub Corner Gtl ... 0 0 0 480 0 1 2008 New Partial 160000
523 524 60 RL 40094 Pave IR1 Bnk AllPub Inside Gtl ... 0 0 0 0 0 10 2007 New Partial 184750

2 rows × 63 columns

1
2
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 523].index)

核心

testing for assumptions underlying the statistical bases for multivariate analysis.

根据Multivariate Data Analysis-Hair et al (2013)，需要进行检验的假设有：

  1. 正态性 Normality
  • 许多统计检验方法都基于正态分布的假设构建的
  • 当样本量大于200时，正态性就不太影响了
  1. 同方差性 Homoskedasticity
  • 误差项通常是独立同方差的
  1. 线性性 Linearity
  • 因变量与自变量之间呈线性关系
  • 如果不是线性关系，可能需要先进行数据变换（data transformation）
  1. 序列自相关性
  • 通常存在于时间序列

正态性检验

  • 直方图
  • 概率密度图(Q-Q图)
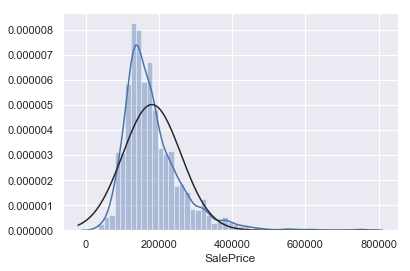
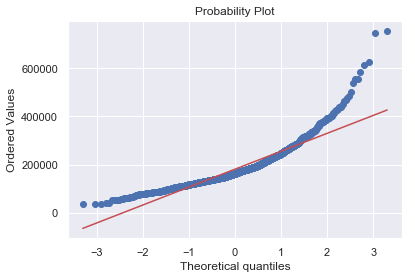
1
2
3
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
  • 很显然，‘SalePrice’并不服从正态分布
  • 右偏
  • QQ图尾部（蓝点）与标准正态分布（红线）不一致
1
2
## 对数据进行对数变换
df_train['SalePrice'] = np.log(df_train['SalePrice'])
1
2
3
4
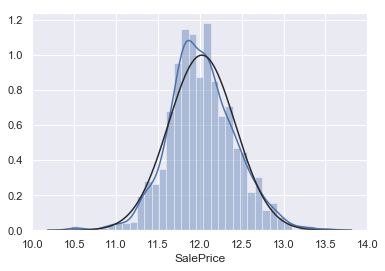
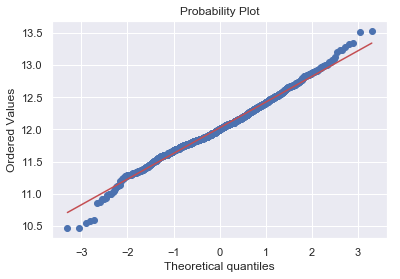
## 检验对数变换后数据的正态性
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

Perfect！

1
2
3
4
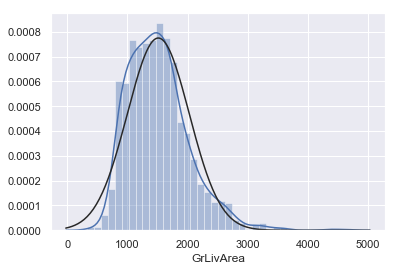
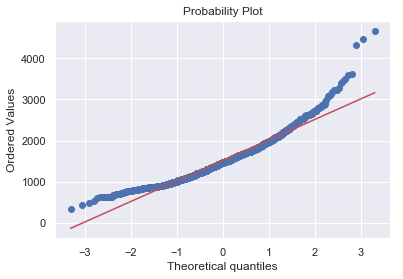
## 再来看看'GrLivArea'
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)
1
2
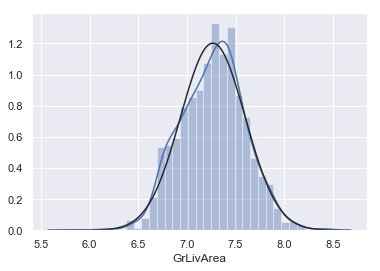
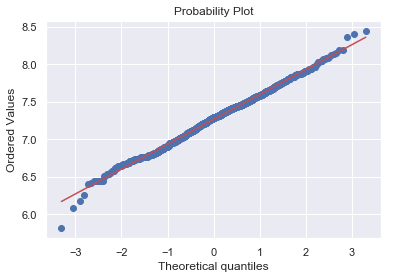
## 进行对数变换
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])
1
2
3
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)
1
2
3
4
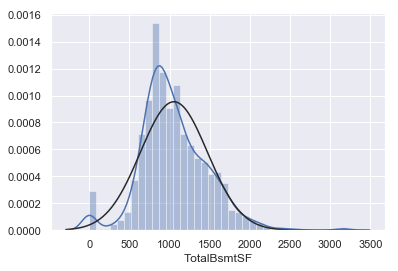
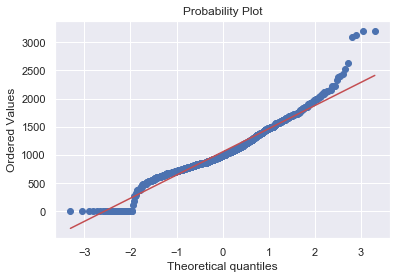
## 'TotalBsmtSF'
sns.distplot(df_train['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)
1
2
3
4
5
6
## 'TotalBsmtSF'存在0值，无法直接进行对数变换
## 只将'TotalBsmtSF'非零值的数据进行对数变换
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0 
df_train.loc[df_train['TotalBsmtSF']>0,'HasBsmt'] = 1
df_train.loc[df_train['HasBsmt']==1,'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])
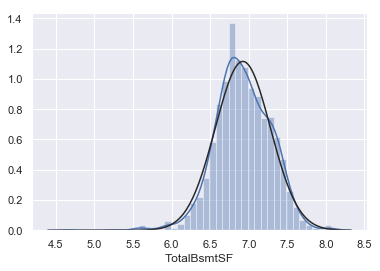
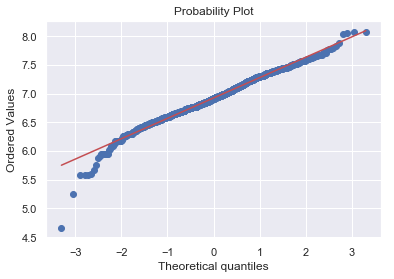
1
2
3
sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)

同方差性（同质性）

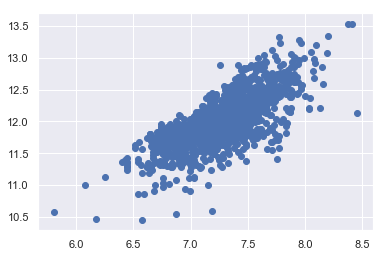
1
plt.scatter(df_train['GrLivArea'], df_train['SalePrice'])
<matplotlib.collections.PathCollection at 0x16f7589eba8>
  • 未进行对数变换前，'GrLivArea’和’SalePrice’散点图呈锥形
  • 进行对数变换后，不再呈锥形（上图）
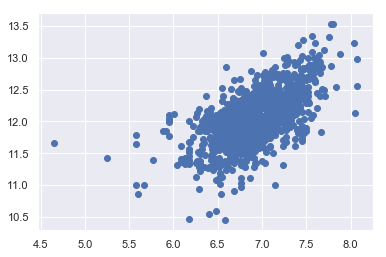
1
plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice'])
<matplotlib.collections.PathCollection at 0x16f7589ebe0>

We can say that, in general, ‘SalePrice’ exhibit equal levels of variance across the range of ‘TotalBsmtSF’.

类别变量

需要将类别变量转化为哑变量（dummy）

1
df_train = pd.get_dummies(df_train)
1
df_train.head()
Id MSSubClass LotArea OverallQual OverallCond YearBuilt YearRemodAdd BsmtFinSF1 BsmtFinSF2 BsmtUnfSF ... SaleType_ConLw SaleType_New SaleType_Oth SaleType_WD SaleCondition_Abnorml SaleCondition_AdjLand SaleCondition_Alloca SaleCondition_Family SaleCondition_Normal SaleCondition_Partial
0 1 60 8450 7 5 2003 2003 706 0 150 ... 0 0 0 1 0 0 0 0 1 0
1 2 20 9600 6 8 1976 1976 978 0 284 ... 0 0 0 1 0 0 0 0 1 0
2 3 60 11250 7 5 2001 2002 486 0 434 ... 0 0 0 1 0 0 0 0 1 0
3 4 70 9550 7 5 1915 1970 216 0 540 ... 0 0 0 1 1 0 0 0 0 0
4 5 60 14260 8 5 2000 2000 655 0 490 ... 0 0 0 1 0 0 0 0 1 0

5 rows × 222 columns

Thank you for your approval.

欢迎关注我的其它发布渠道