Machine Learning | ADMM

Alternating Direction Method of Multipliers

ADMM

交替方向乘子法

• 一种求解可分离的凸优化问题的重要方法
• 处理速度快
• 收敛性能好

原文：Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends® in Machine learning, 2011, 3(1): 1-122.

Basic

共轭函数

Fenchel conjugate function

函数$f(x)$的共轭函数定义为
$$f^{*(y)=\max_x\left{y}Tx-f(x)\right}$$

• 几何意义：共轭函数是切线簇的截距的负值簇
• 如果$f(x)$是凸（convex）的：
  考虑$f(x)$上的点$(x^*,f(x*))$处的斜率为$y^T$的切线
  $$z=y^T(x-x)+f(x^)$$
  该切线的截距项（$x=0$）为
  $$-y^Tx+f(x^)$$
  截距项的负数就是$f(x)$的共轭。
• 如果$f(x)$不是凸（convex）的：
  则切线可能会对应多个截距项

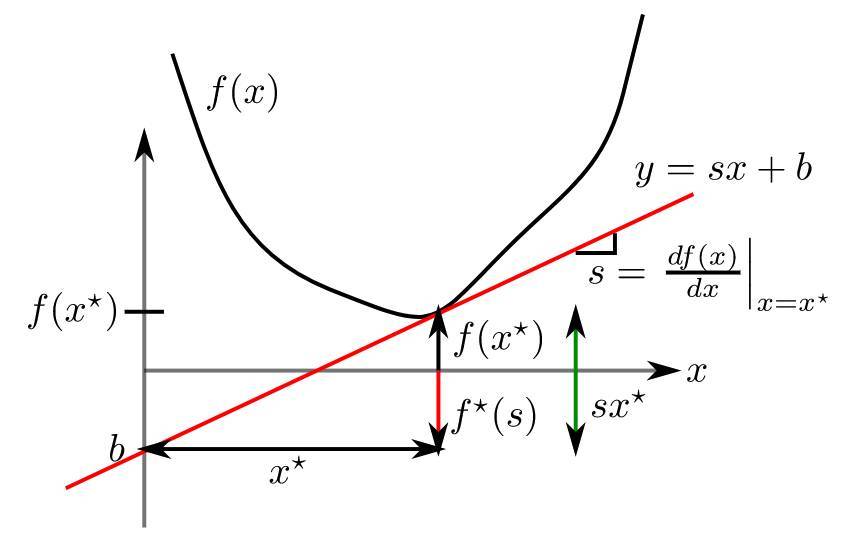
当$f(x)$是严格凸的时，取$z=\arg \max_x {y^Tx-f(x) } $，则有
$$f^(y)=\max_x{ { y^T x-f(x) } }=y^Tz-f(z)$$
因此
$$\nabla f^(y)=z=\arg\max_x { y^Tx-f(x) } =\arg\min_x{ {f(x)-y^Tx } $$

带线性约束的优化问题

考虑带线性约束的优化问题
\begin{equation}
\begin{aligned}
\min & \quad f(x)\
\mathrm{s.t.} & \quad Ax=b
\end{aligned}
\end{equation}
其中$f(x)$是严格凸函数（strictly convex function）。

构造该优化问题的拉格朗日函数
$$L(x,y)=f(x)+y^T(Ax-b)$$
这里$y$是拉格朗日乘子（Lagrangian multiplier）。

求解原优化问题等价于求解
$$\min_x\max_y{L(x,y)}$$

• 当$Ax=b$不成立时，总可以找到$y$使得 $\max_y L(x,y)=\infty$
• 当$Ax=b$成立时，$\min_x\max_y{L(x,y)}=\min_x f(x)$

当$f(x)$可导（differentiable）时，$L(x,y)$分别关于$x,y$求偏导并令偏导数为零，得
$$\left{
\begin{array}{l}
\nabla_x L(x,y) =\nabla f(x)+A^Ty=0\
\nabla_y L(x,y) =Ax-b=0
\end{array}
\right.$$

$\frac{\mathrm{d}(\beta^Tx)}{\mathrm{d}x}=\beta$

$\min_x\max_y{L(x,y)}$的对偶问题（dual problem）是$\max_y\min_x{L(x,y)}$。

当强对偶性^[1]（duality）满足时，$\min_x\max_y{L(x,y)}$与$\max_y\min_x{L(x,y)}$有相同的解。

• Strong duality: Strong duality holds if and only if the duality gap is equal to 0.
  $$p^*=d*$$

• Duality gap: 原始问题（primal problem）的最优解$p^*$与对偶问题（dual problem）的最优解$d^*$之间的差异。
• 强对偶性的充分条件：
• 原始问题是线性优化问题
• $F$是原始函数的perturbation function,$F^{**}$是$F$的biconjugate
  $$F=F^{**}$$
• $F$ is convex and lower semi-continuous
• 凸优化问题的Slater’s condition成立

定义
\begin{equation}
\begin{aligned}
g(y) &= \min_x L(x,y) \
&= \min_x\left{f(x)+y^T(Ax-b)\right}\
&= \min_x\left{f(x)-(-A^Ty)Tx-y^Tb \right}\
&= \underline{\min_x\left{f(x)-(-A^Ty)Tx \right} }-y^Tb\
&= \underline{-f^*(-ATy)}-y^Tb
\end{aligned}
\end{equation}

由于$f^*(y)= \max_x { y^Tx-f(x) } =-\min_x { f(x)-y^Tx } $。

\begin{equation}
\begin{aligned}
\nabla g(y) &= A\nabla f^*(-ATy)-b\
&= A\arg\min_x\left{f(x)+y^TAx \right}-b\
&= A\arg\min_x\left{f(x)+y^T(Ax-b) \right}-b\
&= A\arg\min_x L(x,y)-b
\end{aligned}
\end{equation}

$\frac{\mathrm{d}(x^T\beta)}{\mathrm{d}x}=\beta$

DAM

Dual Decomposition
Dual Ascent Algorithm
对偶上升算法

算法的第$k+1$步迭代为

\begin{equation}
\begin{aligned}
x^{k+1}&=\arg\min_x L(x,y^k)\
y^{k+1}&=y{k} + \alpha^k\nabla g(y^k) \quad \mathrm{(Gradient Ascent Update)}\
&= y^k + \alpha^k(Ax{k+1}-b)
\end{aligned}
\end{equation}
其中

• $\alpha^k>0$是步长
• $\nabla g(y^k)=A\arg\min_x L(x,y^k)-b$

当$f(x)$可分时，即
$$f(x)=\sum_{i=1}^nf_i(x_i)$$
则
\begin{equation}
\begin{aligned}
L(x,y^k) &= f(x)+y^T(Ax-b)\
&= \sum_{i=1}^nf_i(x) + y^{T\left(\sum_{i=1}}nA_ix_i-b\right)\
&=\sum_{i=1}^{n\left(f_i(x)+y}TA_ix_i-\frac{1}{n}y^Tb \right)\
&= \sum_{i=1}^nL_i(x_i,yk)
\end{aligned}
\end{equation}

则分成了$n$个平行计算
$$x_i^{k+1}=\arg\min_{x_i} L_i(x_i, y^k)$$

ALM

Augmented Lagrangian Method
Method of Multipliers
增广的拉格朗日乘子法

当$f(x)$不是严格凸时，Dual Ascent Algorithm不适用。

增广的拉格朗日函数为
$$L_\rho(x,y)=f(x)+y^{T(Ax-b)+\frac{\rho}{2}||Ax-b||}2$$
即解决优化问题
\begin{equation}
\begin{aligned}
\min & \quad f(x)+\frac{\rho}{2}||Ax-b||^2\
\mathrm{s.t.} &\quad Ax=b
\end{aligned}
\end{equation}

则
\begin{equation}
\begin{aligned}
x^{k+1} &= \arg\min_x{L_\rho(x,y^k)}\
y^{k+1} &= y^k + \rho(Ax^{k+1}-b)
\end{aligned}
\end{equation}

为什么步长为$\rho$？
我们只考虑$f(x)$可导的特殊情况。
原始优化问题如果满足：
\begin{equation}
\begin{aligned}
\nabla_x L(x^*,y*) &= \nabla f(x^*)+ATy^*=0\
\nabla_y L(x^*,y*) &= Ax^*-b=0
\end{aligned}
\end{equation}
则称为primal and dual feasibility。
因为$x^{{k+1}=\arg\min_xL_\rho(x,y}k)$，所以
\begin{equation}
\begin{aligned}
0 &= \nabla_x L_\rho(x^{k+1},yk)\
&= \nabla_x f(x^{k+1})+AT(y^k+\rho(Ax{k+1}-b))
\end{aligned}
\end{equation}
如果取$y^{k+1}=yk+\rho(Ax^{k+1}-b)$，则有
$$\nabla_xf(x^{k+1})+ATy^{k+1}=0$$
所以，如果取步长为$\rho$，则可以保证每一次迭代后的解都满足dual feasible.

与Dual Ascent Method相比，

• ALM需要的假设相对比较不严格，且有更好的收敛性
• 但是ALM不能并行计算，即使$f(x)$可分

ADMM

用于解决如下问题
\begin{equation}
\begin{aligned}
\min & \quad f(x)+g(z)\
\mathrm{s.t.} & \quad Ax+Bz=c
\end{aligned}
\end{equation}

该优化问题的扩展拉格朗日函数为
$$L_\rho(x,y,z)=f(x)+g(z)+y^{T(Ax+Bz-c)+\frac{\rho}{2}||Ax+Bz-c||}2$$
其中$\frac{\rho}{2}||Ax+Bz-c||^2$是扩展项（augmented term）。

使用ALM解上述问题：
\begin{equation}
\begin{aligned}
(x^{k+1},z{k+1}) &= \arg\min_{x,z} L_\rho (x,z,y^k)\
y^{k+1} &= y^k + \rho (Ax^{k+1}+Bz{k+1}-c)
\end{aligned}
\end{equation}

ADMM与ALM的区别：
ADMM将ALM中的$(x,z)-$最小化步骤拆分成两步：

• x-minimization
• z-minimization
  \begin{equation}
  \begin{aligned}
  x^{k+1} &= \arg\min_x L_\rho(x,z^k,yk)\
  z^{k+1} &= \arg\min_z L_\rho(x^{k+1}, z,y^k)\
  y^{k+1} &= y^k+\rho(Ax{k+1}+Bz^{k+1}-c)
  \end{aligned}
  \end{equation}

定义残差项$r=Ax+Bz-c$，则$L_\rho(x,y,z)$可改写为
\begin{equation}
\begin{aligned}
L_\rho(x,y,z) &= f(x)+g(z)+y^{T(Ax+Bz-c)+\frac{\rho}{2}||Ax+Bz-c||}2\
&= f(x)+g(z)+y^{Tr+\frac{\rho}{2}||r||}2\
&= f(x)+g(z)+\frac{\rho}{2}||r+\frac{1}{\rho}y||^{2-\frac{1}{2\rho}||y||}2\
&= f(x)+g(z)+\frac{\rho}{2}||r+u||^{2-\frac{\rho}{2}||u||}2
\end{aligned}
\end{equation}
其中

• $u=\frac{1}{\rho}y$称为scaled dual variable
• \begin{aligned}
  \frac{\rho}{2}||r+\frac{1}{\rho}y||^2 &= \frac{\rho}{2}\left(||r||^{2+\frac{2}{\rho}y}Tr+\frac{1}{\rho^2}||y||2 \right)\
  &= \frac{\rho}{2}||r||^2+yTr+\frac{1}{2\rho}||y||^2
  \end{aligned}

则ADMM的迭代步骤变为
\begin{aligned}
x^{k+1} &= \arg\min_x \left{f(x)+\frac{\rho}{2}||Ax+Bz^k-c+uk||^2 \right}\
z^{k+1} &= \arg\min_z \left{g(z)+\frac{\rho}{2}||Ax^{k+1}+Bz-c+uk||^2 \right}\
u^{k+1} &= u^k+Ax{k+1}+Bz^{k+1}-c
\end{aligned}

收敛性

基于两个假设证明ADMM的收敛性

• 假设1：函数$f:\mathbb{R}^n\rightarrow \mathbb{R}\cup {+\infty}$和函数$g:\mathbb{R}^m\rightarrow\cup {+\infty}$是closed, proper and convex.

该假设保证了x-minimization step和z-minimization step有解

• 假设2：非增广德拉格朗日函数$L_0$有一个鞍点（saddle point）

该假设意味着存在$(x^*,z*,y^*)$（并不要求唯一）。
$$L_0(x^*,z,y)\leq L_0(x^, z^, y^) \leq L_0(x, z, y^*)$$
对所有的$x,z,y$成立

• $y^*=\arg\max L_0(x^*,z*,y)$
• $(x^*,z*)=\arg\min L_0(x,z,y^*)$

基于上述两个假设，ADMM迭代满足：

• 残差收敛：
  $$r^k\rightarrow 0\quad (k\rightarrow \infty)$$
• 目标函数收敛：
  $$f(x^k)+g(xk)\rightarrow p^* \quad (k\rightarrow\infty)$$
• 对偶变量(Dual Variable)收敛：
  $$y^k\rightarrow y^* \quad (k\rightarrow \infty)$$

Optimality Conditions

ADMM最优化的充要条件是primal feasibility
$$Ax^*+Bz-c=0$$
和dual feasibility
$$\nabla f(x^*)+ATy^=0$$
$$\nabla g(z^*)+BTy^*=0$$

$$L_\rho(x,y,z) = f(x)+g(z)+y^{T(Ax+Bz-c)+\frac{\rho}{2}||Ax+Bz-c||}2$$

• 因为$z^{k+1}=\arg\min_z L_\rho(x^{k+1}, z, y^k)$，所以有
  \begin{aligned}
  0 &= \nabla_z L_\rho(x^{k+1}, z^{k+1}, y^k)\
  &= \nabla g(z^{k+1})+BTy^k+\rho B^T(Ax{k+1}+Bz^{k+1}-c)\
  &= \nabla g(z^{k+1})+BTy^k+\rho B^Tr{k+1}\
  & \left(因为y^{k+1}=yk+\rho(Ax^{k+1}+Bz{k+1}-c)=y^k+\rho r^{k+1}\right)\
  &= \nabla g(z^{k+1})+BTy^{k+1}
  \end{aligned}
  所以，每次迭代结束后总满足$\nabla g(z)+B^Ty=0$。
• 因为$x^{k+1}=\arg\min_x L_\rho(x,z^k,yk)$，所以有
  \begin{aligned}
  0 &= \nabla_x L_\rho(x^{k+1},zk,y^k)\
  &= \nabla f(x^{k+1}) + A^Tyk+\rho A^T(Ax{k+1}+Bz^k-c)\
  &= \nabla f(x^{k+1})+AT(y^k+\rho r^{k+1}+\rho B(z^k-z{k+1}))\
  &= \nabla f(x^{k+1})+ATy^{k+1}+\rho A^TB(zk-z^{k+1})
  \end{aligned}
  等价于
  $$\rho A^TB(z{k+1}-z^k)=\nabla f(x^{k+1})+ATy^{k+1}$$

Stopping Criterion

$$||Ax^k+Bzk-c||^2=||rk||^2\leq \epsilon^{pri}$$
$$||\rho A^TB(z{k+1}-z^k)||2=||s^k||2\leq \epsilon^{dual}$$
其中$\epsilon^{{pri}>0$,$\epsilon}{dual}>0$是feasibility tolerances。
可取
\begin{aligned}
\epsilon^{pri} &= \sqrt{p}\epsilon^{{abs}+\epsilon}{real}\max{||Ax^k||2, ||Bz^k||2, ||c||^2 }\
\epsilon^{dual} &= \sqrt{n}\epsilon^{{abs}+\epsilon}{real}||A^Tyk||^2
\end{aligned}
其中$\epsilon^{{real}$可取$\epsilon}{real}=\frac{1}{10}$。

应用

求解LASSO

给定$y\in \mathbb{R}^{n,\mathbf{X}\in\mathbb{R}}{n\times p}$，LASSO问题为
$$\min \quad \frac{1}{2}||y-\mathbf{X}\beta||^2+\lambda||\beta||_1$$
可以写成
\begin{aligned}
\min & \quad \frac{1}{2}||y-\mathbf{X}\beta||^2+\lambda||\alpha||_1\
\mathrm{s.t.} & \quad \beta-\alpha=0
\end{aligned}

对应的拉格朗日函数为
$$L_\rho(\alpha,\beta,\phi)=\frac{1}{2}||y-\mathbf{X}\beta||^{2+\lambda||\alpha||_1+\phi}T(\beta-\alpha)+\frac{\rho}{2}||\beta-\alpha||^2$$
其中$\phi$是拉格朗日乘子,$y$是response。

增广的拉格朗日函数为
$$L_\rho(\alpha,\beta,u)=\frac{1}{2}||y-\mathbf{X}\beta||^{2+\lambda||\alpha||_1+\phi}T(\beta-\alpha+u)-\frac{1}{2\rho}||u||^2$$

LASSO问题的ADMM为
\begin{aligned}
\beta^{k+1} &= \arg\min_\beta\left{\frac{1}{2}||y-\mathbf{X}\beta||^{2+\frac{\rho}{2}||\beta-\alpha}k+u^k||2\right}\
\alpha^{k+1} &= \arg\min_\alpha\left{\lambda||\alpha||_1+\frac{\rho}{2}||\beta^{{k+1}-\alpha+u}k||^2\right}\
u^{k+1} &= u^k+\beta{k+1}-\alpha^{k+1}
\end{aligned}
其中$u^{k=\frac{1}{\rho}\phi}k$。

对于$\beta^{k+1} = \arg\min_\beta\left{\frac{1}{2}||y-\mathbf{X}\beta||^{2+\frac{\rho}{2}||\beta-\alpha}k+u^k||2\right}$有
\begin{aligned}
& \frac{\partial{\left{\frac{1}{2}||y-\mathbf{X}\beta||^{2+\frac{\rho}{2}||\beta-\alpha}k+u^k||2\right} }}{\partial{\beta} }\
= & \mathbf{X}(\mathbf{X}\beta-y)+\rho(\beta-\alpha^k+uk)\
= & (\mathbf{X}^T\mathbf{X}+\rho\mathbf{I} )\beta-\left[\mathbf{X}^{Ty+\rho(\alpha}k-u^k) \right]\
= & 0
\end{aligned}
则有
$$\beta^{{k+1}\triangleq(\mathbf{X}}T\mathbf{X}+\rho\mathbf{I})^{{-1}\left(\mathbf{X}}Ty+\rho(\alpha^k-uk) \right)$$

对于$\alpha^{k+1} = \arg\min_\alpha\left{\lambda||\alpha||_1+\frac{\rho}{2}||\beta^{{k+1}-\alpha+u}k||^2\right}$有
\begin{aligned}
& \frac{\partial{\lambda|\alpha_j|+\frac{\rho}{2}(\beta_j^{{k+1}-\alpha_j+u_j}k)^2} }{\partial{\alpha_j} }\
= & \lambda \mathrm{sgn}(\alpha_j)-\rho(\beta_j^{k+1}+u_jk-\alpha_j)
\end{aligned}

• 当$\alpha_j>0$时，如果有$\beta_j^{k+1}+u_jk>\frac{\lambda}{\rho}$，则有
  $$\alpha_j^{{k+1}=\beta_j}{k+1}+u_j^k-\frac{\lambda}{\rho}$$
• 当$\alpha_j=0$时，$\alpha_j^{k+1}=0$
• 当$\alpha_j<0$时，如果有$\beta_j^{k+1}+u_jk+\frac{\lambda}{\rho}<0$，则有
  $$\alpha_j^{{k+1}=\beta_j}{k+1}+u_j^k+\frac{\lambda}{\rho}$$

最后，有
$$\alpha_j^{k+1}=S_{\frac{\lambda}{\rho} }\left(\beta_j^{k+1}+u_jk \right)$$
其中$S_{\frac{\lambda}{\rho} }$为soft thresholding function
$$S_{\kappa}(a)=\left{
\begin{array}{ll}
a-\kappa & a>\kappa\
0 & |a|\leq\kappa\
a+\kappa & a<-\kappa
\end{array}
\right.$$
其中$\kappa=\frac{\lambda}{\rho}$。

因此，LASSO问题的ADMM(显式)迭代过程为
\begin{aligned}
\beta^{k+1} &= (\mathbf{X}^{T\mathbf{X}+\rho\mathbf{I})}{-1}\left(\mathbf{X}^{Ty+\rho(\alpha}k-u^k) \right)\
\alpha^{k+1} &= S_{\frac{\lambda}{\rho} }\left(\beta^{k+1}+uk \right)\
u^{k+1} &= u^k+\beta{k+1}-\alpha^{k+1}
\end{aligned}
Stopping Criterion可以为
$$||\beta^{k+1}-\alpha{k+1}||<\epsilon$$
或
$$\rho ||\alpha^{k+1}-\alphak||<\epsilon$$

求解Fused LASSO

Fused LASSO为
$$\min\quad \frac{1}{2}||y-\mathbf{X}\beta||^{2+\lambda_1||\beta||_1+\lambda_2\sum_{i=2}}p|\beta_i-\beta_{i-1}|$$
是广义LASSO的一般形式。

可以改写为
$$\min\quad \frac{1}{2}||y-\mathbf{X}\beta||^{2+\lambda_1||D\beta||}2$$
其中
$$D=\left(
\begin{array}{c}
\mathbf{I}_p\
B
\end{array}
\right)$$
$$B=\frac{\lambda_2}{\lambda_1}\left(
\begin{array}{cccccc}
-1 & 1 & 0 & \cdots & 0 & 0\
0 & -1 & 1 & \cdots & 0 & 0\
0 & 0 & -1 & \cdots & 0 & 0\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots\
0 & 0 & 0 & \cdots & 1 & 0\
0 & 0 & 0 & \cdots & -1 & 1
\end{array}
\right)$$

Fused LASSO可以进一步写为
\begin{aligned}
\min & \quad \frac{1}{2}||y-\mathbf{X}\beta||^2+\lambda||\alpha||_1\
\mathrm{s.t.} & \quad D\beta-\alpha=0
\end{aligned}

则Fused LASSO的ADMM迭代步骤为
\begin{aligned}
\beta^{k+1} &= (\mathbf{X}^T\mathbf{X}+\rho D^TD){-1}\left(\mathbf{X}^Ty+\rho D^T(\alphak-u^k) \right)\
\alpha^{k+1} &= S_{\frac{\lambda}{\rho} }(D\beta^{k+1}+uk)\
u^{k+1} &= u^k+D\beta{k+1}-\alpha^{k+1}
\end{aligned}

上述算法可以解决不同的广义LASSO问题（$D$不同）。

参考资料

• W. Zhong, J. Lin - Statistical Data Analysis
• 最强Fenchel对偶解读
• [Algorithm]ADMM简明理解
• 交替方向乘子法（ADMM）算法的流程和原理是怎样的？

---

1. 强对偶性：若原始问题（对偶问题）有一个确定的最优解，那么对偶问题（原始问题）也有一个确定的最优解，而且这两个最优解所对应的目标函数值相等。 ↩︎